PDF大数据统计方法分析新冠肺炎
使用exensio 软件可以模拟、观察、统计疫情的发展情况。例如,取2月1日到2月13日的数据,在exensio中可以绘制动态折线图,动态展示全国新增确诊病例,新增死亡病例,新增出院病例随时间的变化。同时可以绘制全国疫情地图,动态展示各省市疫情发展状况,并且点击选取各省,可出现此省各市疫情情况。通过每个省份每百万感染率,可以得到各省感染人数在总人数中的占比,从而分析全国省份疫情严重程度。

(exensio制作的动态图)
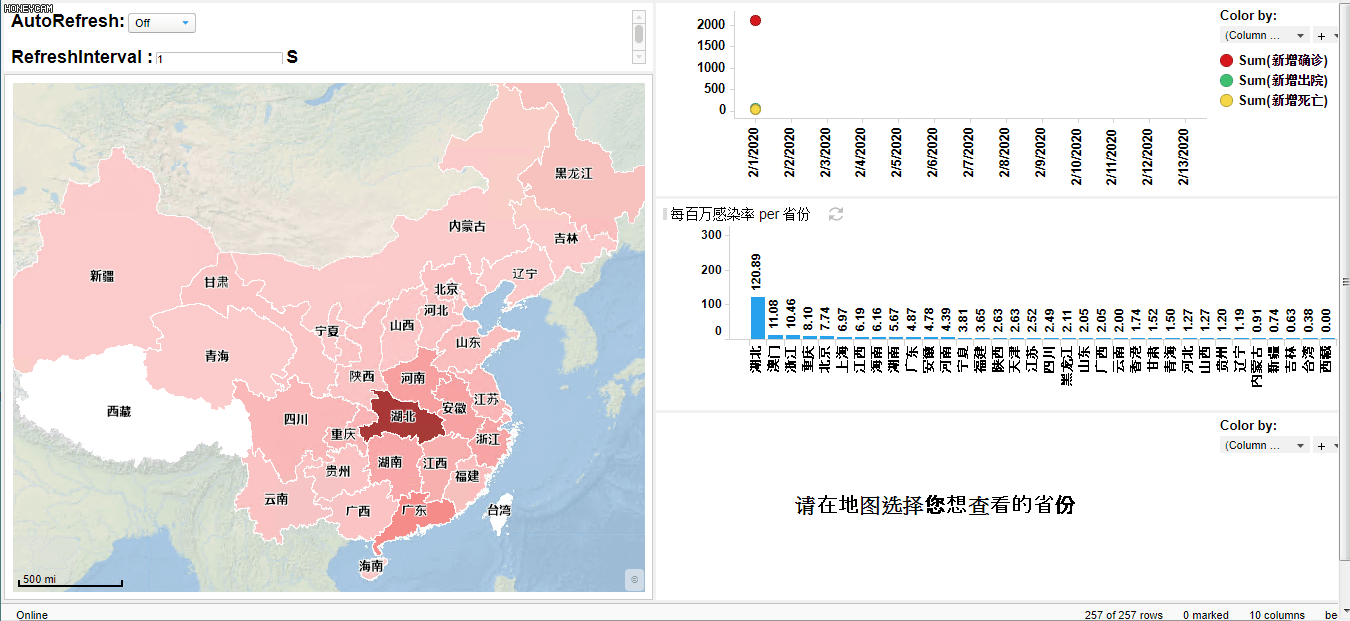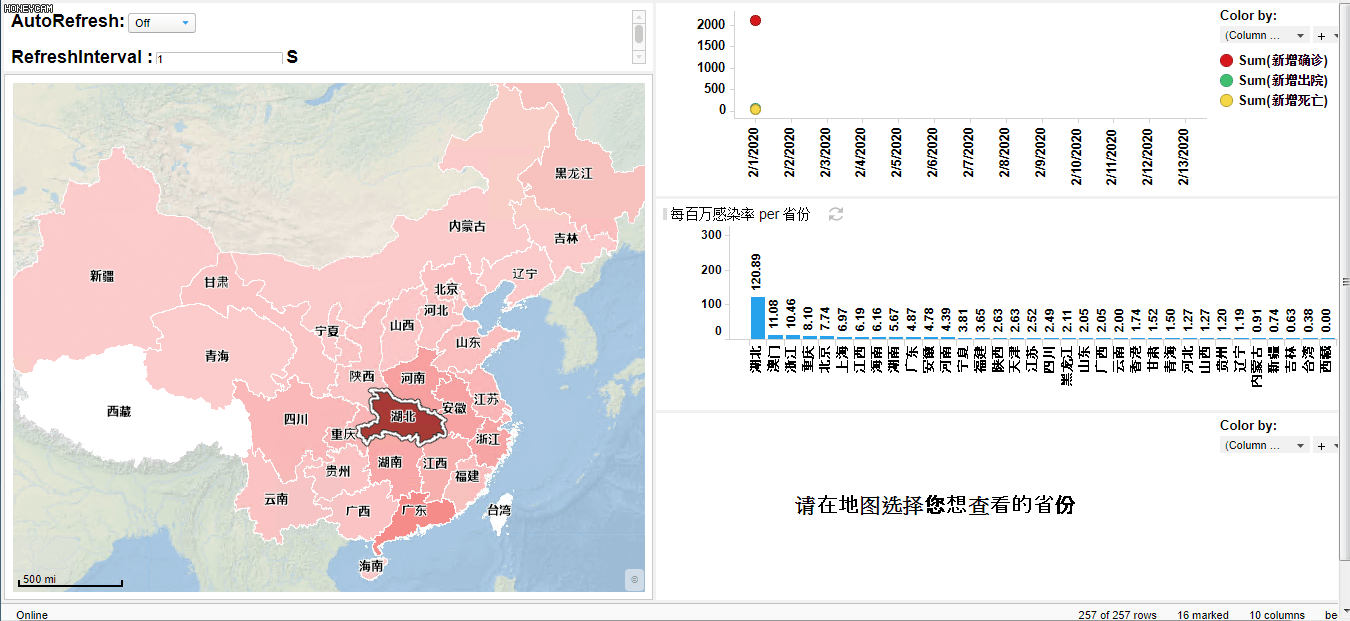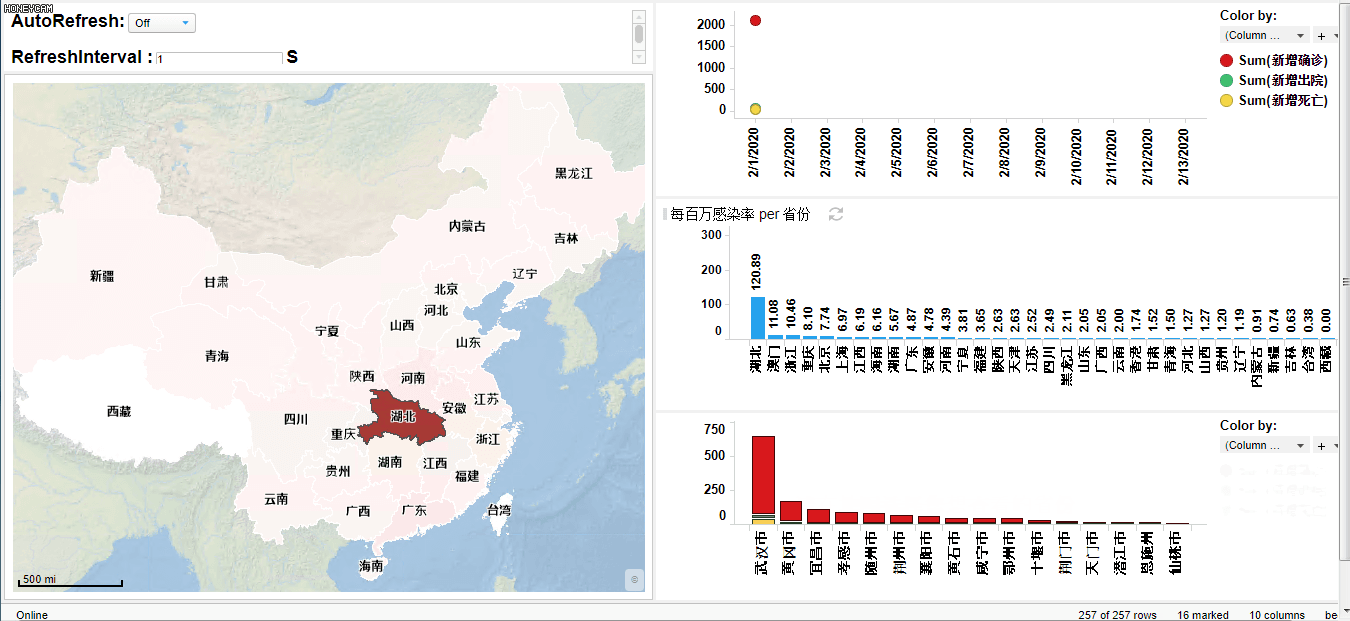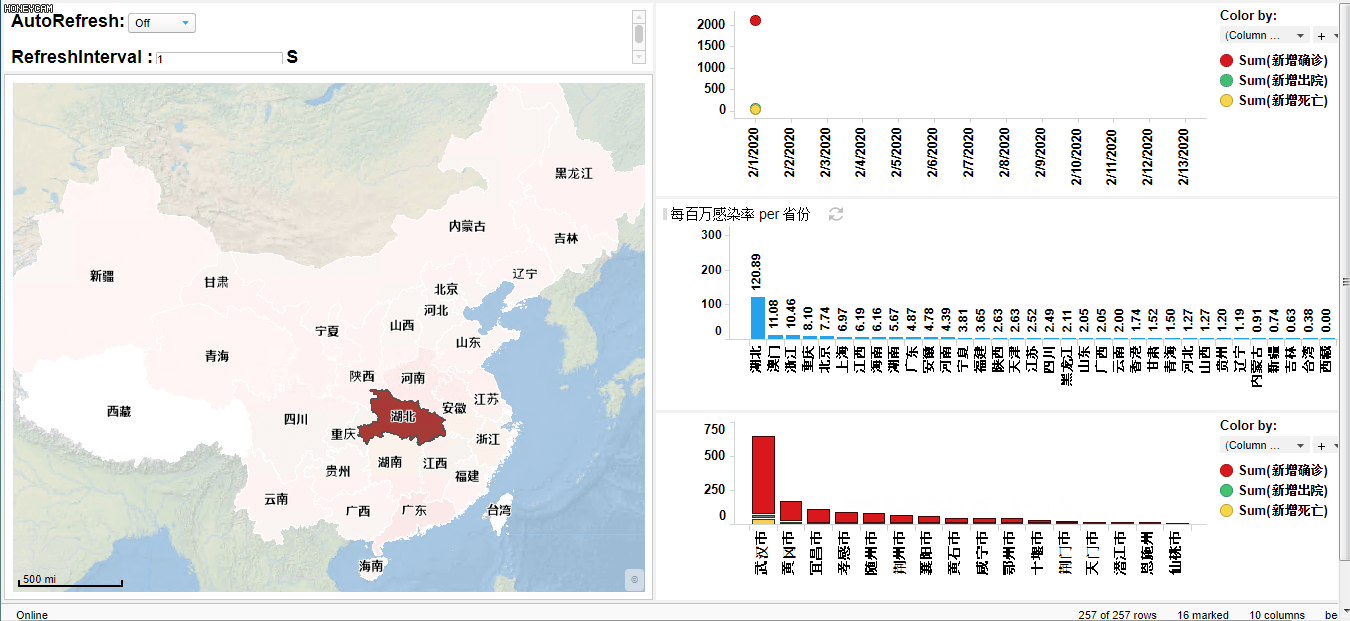
(exensio制作的动态图)
在此过程中可以发现,2月13号时新增确诊病例数激增,查证新闻得知,湖北新增突然上升,因诊断标准发生更改。因湖北省病例数量远高于其他各省,因此在后续统计分析中,我们使用除湖北省外其他各省数据。在exensio中可以同样可以绘制各省数据动态变化图。
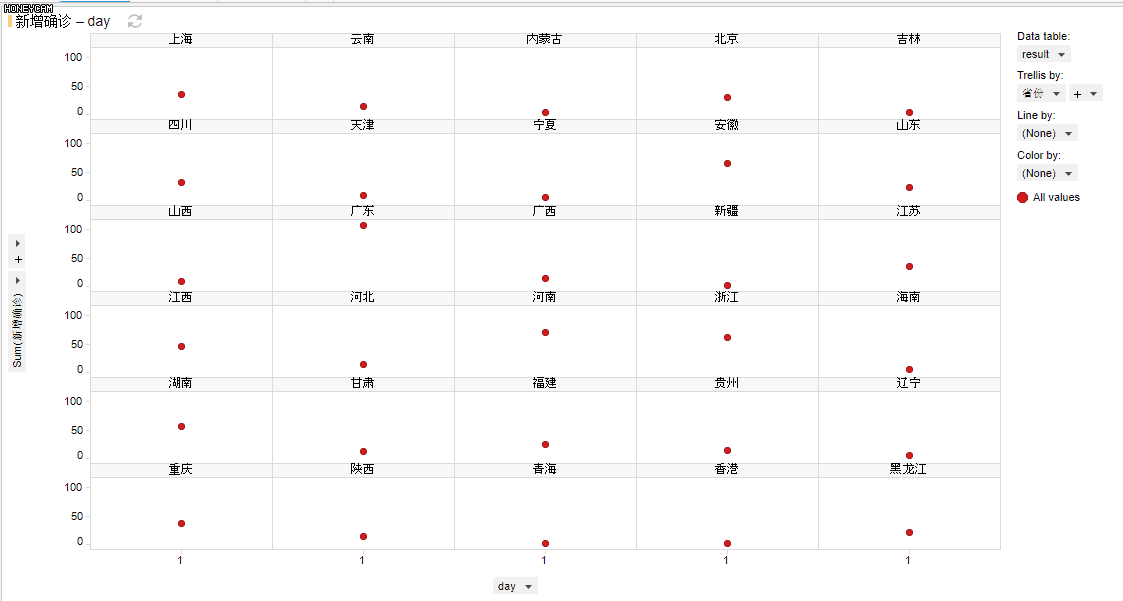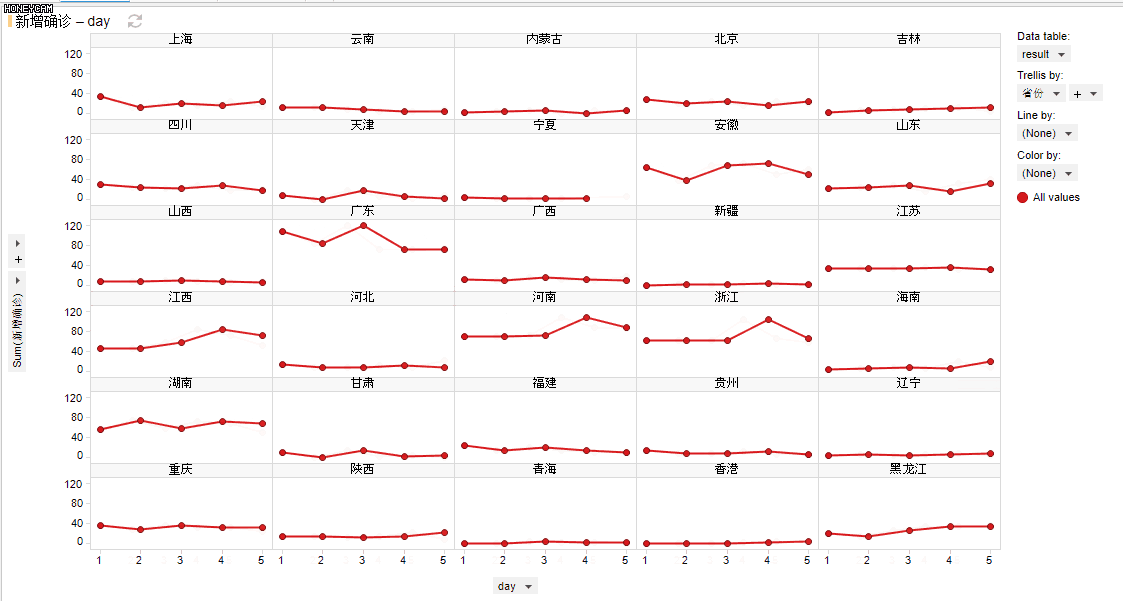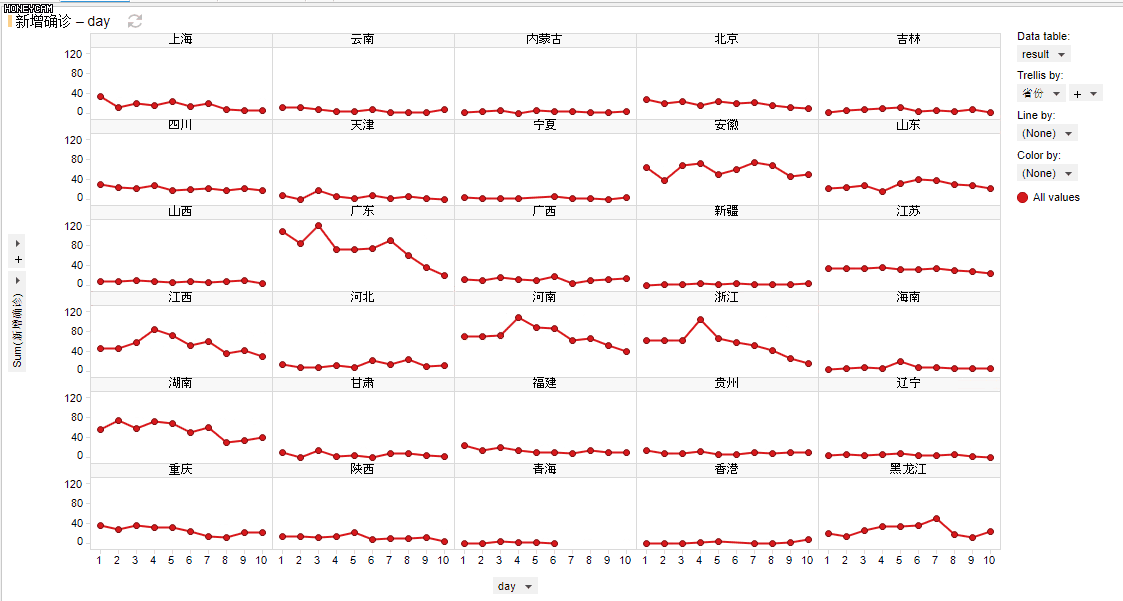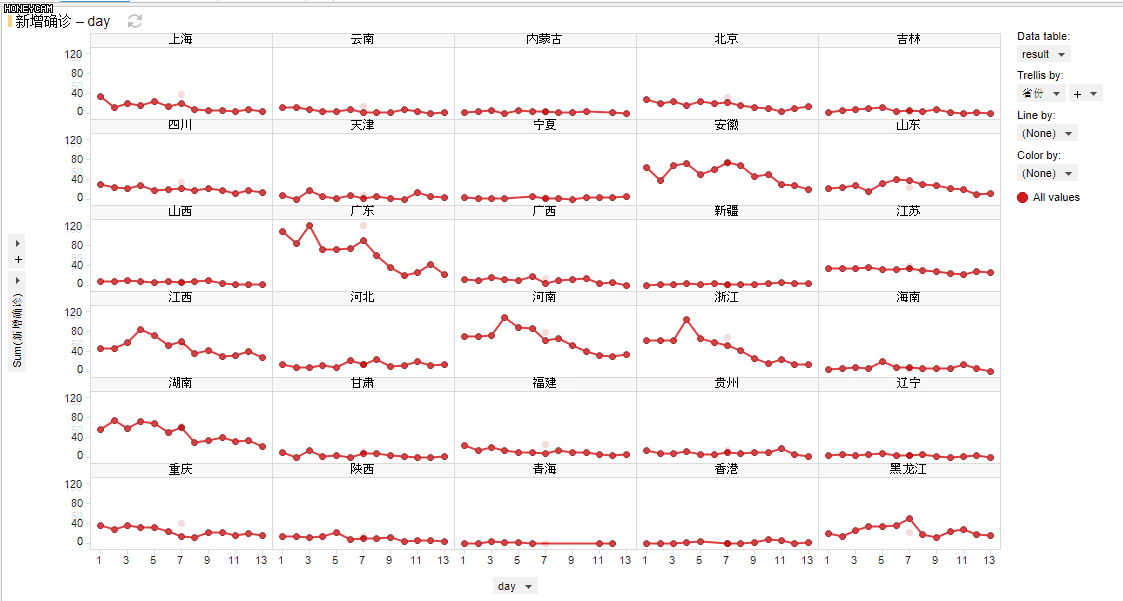
(exensio制作的动态图)
在大数据分析中,回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析,时间序列模型以及发现变量之间的因果关系。因此,这次疫情,我们可以用回归方法进行分析预测。
我们使用2月1日到2月13日除湖北省外其他各省的新增病例数进行线性回归分析, 线性回归是数理统计中常用的回归分析,是用来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。我们使用时间做为X轴,人数做为Y轴,模拟出线性回归曲线。
然而一般来说,两个变量之间的关系是十分微妙的,仅仅采用简单的直线、曲线参数方程去描述是不够的,因此可以采用局部加权回归,它是一种用于局部回归分析的非参数方法,主要是把样本划分成一个个小区间,对区间中的样本进行多项式拟合,不断重复这个过程得到在不同区间的加权回归曲线,最后再把这些回归曲线的中心连在一起合成完整的回归曲线。
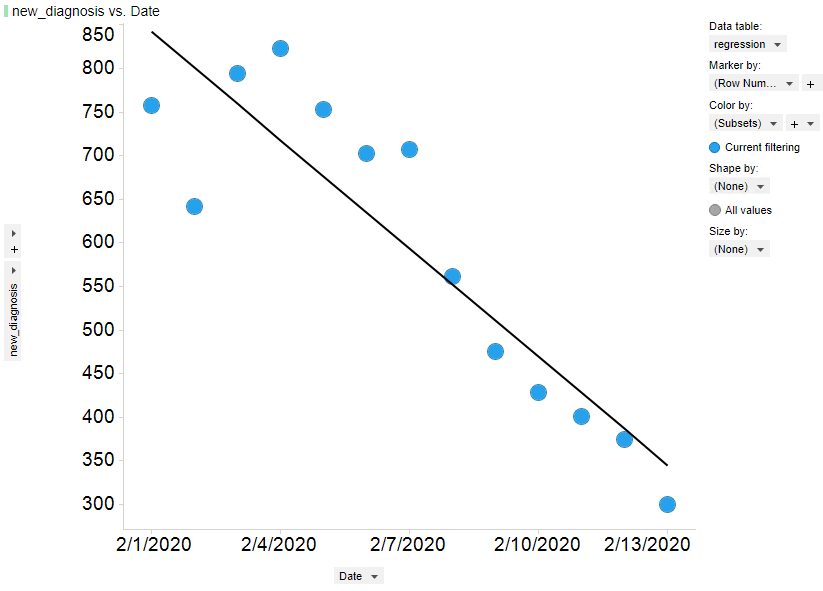
(线性回归新增确诊人数随日期变化)
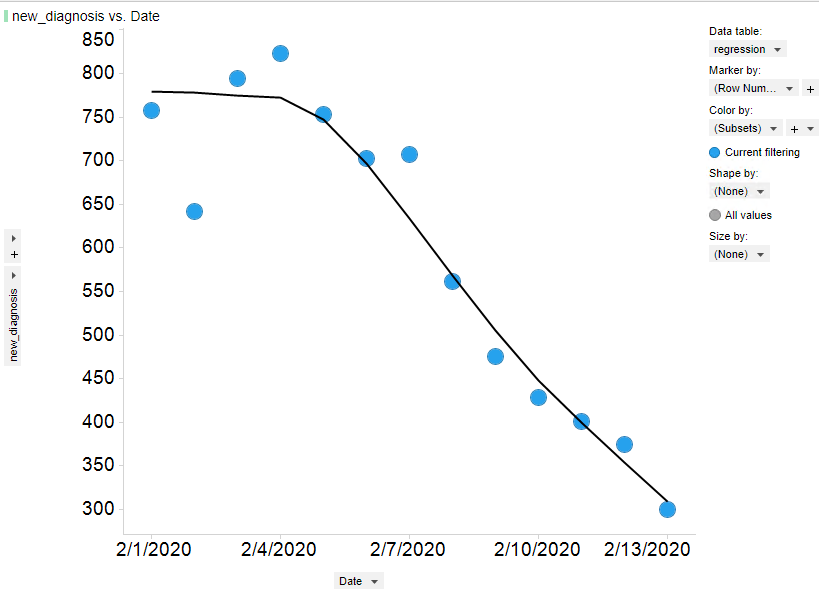
(局部加权回归新增确诊人数随日期变化)
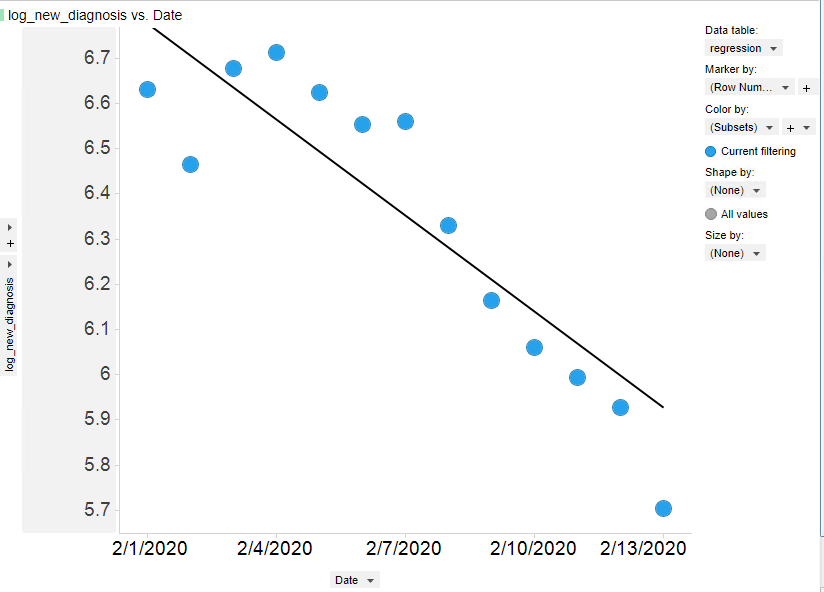
(泊松回归新增确诊人数的对数随日期变化)
除了上述提及的,还有很多常用的回归分析方法,它们适用于不同类型的数据以及不同应用场景,例如专门针对计数数据的泊松回归。
Poisson模型(泊松回归模型)是基于泊松分布,用于描述单位时间、单位面积或者单位容积内某事件发现的频数分布情况,使用新增确诊人数的对数做为Y轴,时间做为X轴,可以模拟出泊松回归曲线。
通过以上回归模型,可以模拟出新增确诊人数随时间变化规律,从而对预测疫情发展走向,预测疫情结束时间产生帮助。